Prim's Algorithm is a greedy algorithm that finds a minimum spanning tree for weighted undirected graphs.
Spanning Trees:
Retain a minimal set of edges so that graphs remain connected. A tree is a minimally connected graph. Adding an edge to a tree creates a loop and removing an edge disconnects the graph.
In this graph, the red edges form a Spanning tree
Minimum Cost Spanning Tree:
- Add the cost of all the edges in the Tree
- Amount different spanning trees, choose the one with a minimum one
Finding Minimum Cost Spanning Trees using Prim's Algorithm
Strategy:
- Incrementally grow the minimum cost spanning tree
- Start with the smallest weight edge overall
- Extend the current tree by adding the smallest edge from the vertex of the tree to a vertex not yet reached
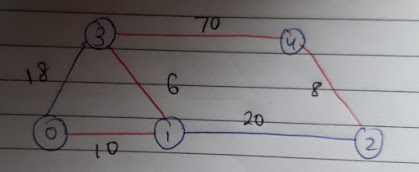
For example, consider:
Start with the smallest edge which is between Vertex 1 and Vertex 3 in the above given example.
After this, we can extend the tree by choosing edges that are connected with Vertex 1 and Vertex 3. This means we have the option of extending the tree by choosing the edge-
- Between Vertex 3 and Vertex 0
- Between Vertex 1 and Vertex 0
- Between Vertex 1 and Vertex 2
- Between Vertex 3 and Vertex 4
We extend the tree from the edge between Vertex 1 and Vertex 0 because that is the smallest edge out of the four.
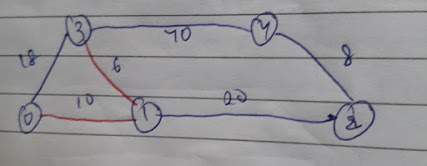
Notice that the smallest edge is of weight 18 which connects Vertex 0 and Vertex 3. However, if we add this edge, it will form a cycle and thus we extend the tree by choosing the edge between Vertex 1 and Vertex 2, which is the second smallest edge.
Finally, we select the edge between Vertex 2 and Vertex 4 which has a weight of 8. Thus, this is how we found a Minimum Spanning Tree using Prim's Algorithm
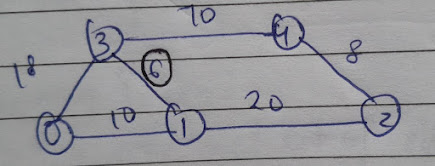


Comments
Post a Comment